Die Leiter berührt die Wand in einer Höhe von 4,8385… Metern.

Allgemeine Lösung:

Eine Leiter der Länge L stehe so gegen eine Wand gelehnt, daß sie einen Würfel der Kantenlänge a, der an der Wand steht, berührt. In welcher Höhe berührt die Leiter die Wand?

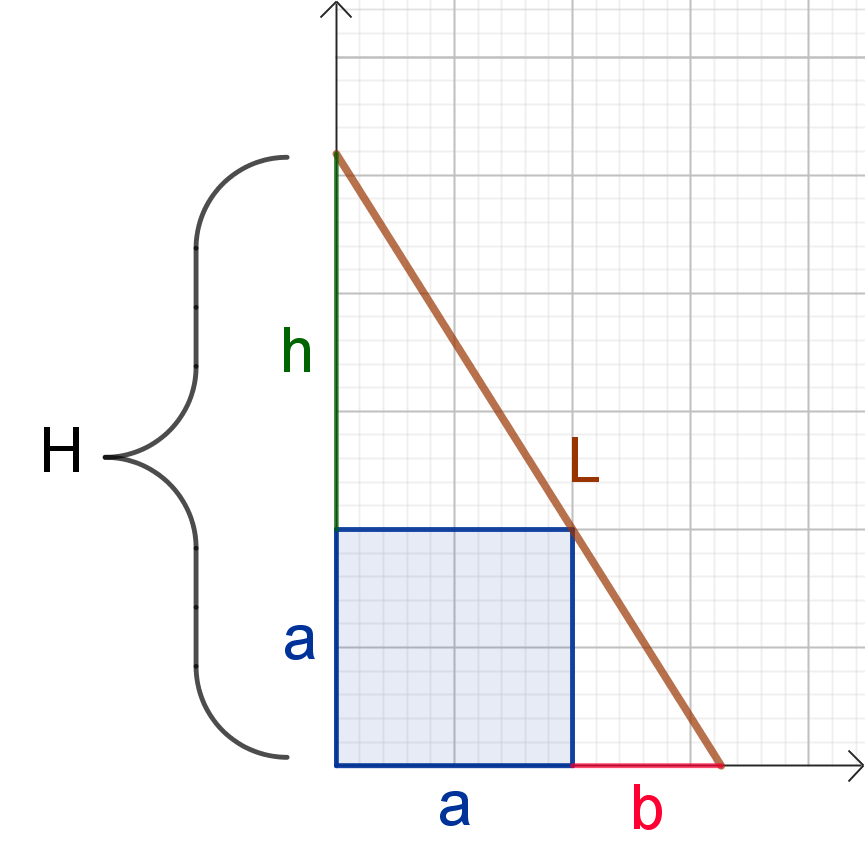
Interpretiert man die Leiter als Stück einer Geraden, sieht man am Steigungsdreieck  a/h = b/a, also b = a²/h.

Nach dem Satz von Pythagoras gilt

(a + h)² + (a + b)² = L²,

also: (a + h)² + (a + a²/h)² = L²
a² + 2ah + h² + a² + 2a³/h + a⁴/h² = L²
h² + 2a² + a⁴/h² + 2ah + 2a³/h = L²
(h + a²/h)² + 2a(h + a²/h) = L²

Variablensubstitution x := h + a²/h führt auf die Gleichung:

x² + 2ax – L² = 0

Das ist ein quadratisches Polynom in x. Die beiden Lösungen in x lauten:

x₁ = -a + √(a² + L²) und x₂ = -a – √(a² + L²)

x = h + a²/h löst man nun nach h auf, um die Lösung in h zu erhalten:

h² – xh + a² = 0

Das ist ein quadratisches Polynom in h. Die beiden Lösungen dieser Gleichung in h sind:

h₁ = x/2 + √(x²/4 – a²) und h₂ = x/2 – √(x²/4 – a²)

Eine gültige Lösung ist die Kombination x₁, h₁, da die Lösung zu dieser Kombination positiv ist.

h₁ = (-a + W)/2 + √(-a²/2 + L²/4 – aW/2),

mit W: = √(a² + L²)
Also ist 

H₁ := h₁ + a = (W + a)/2 + √(L²/4 – (a/2)(a + W)) 

eine Lösung, W wie oben.
Die Kombination x₁, h₂ liefert auch eine Lösung und zwar die zweite Lösung gemäß der Stellung der Leiter – steil oder flach (welche identisch ist mit dem b aus der ersten Lösung aus Symmetriegründen). Die Kombinationen mit x₂ liefern keine gültige Lösungen, da negativ.
Rechenbeispiel: L = 5, a = 1: 
Man erhält H =  (√(26) + 1)/2 + √(25/4 – 0,5(1 + √(26))) ~ 4,8385