Die Wiese hat den Radius 10 m. Im Koordinatensystem können wir die untere Hälfte des Kreises darstellen durch den Graphen von g mit g(x) = 10 – √(100-x²).

Der Pflock für die Leine steckt auf dem Rand der Wiese im Punkt P₀. Der Kreis, den die ständig an der Leine der Länge r zerrende Ziege beschreibt, schneidet den Rand der Lichtung in zwei Punkten P₁ und P₂.

Wir beschreiben ihn durch den Graphen von f mit f(x) = √(r²-x²).

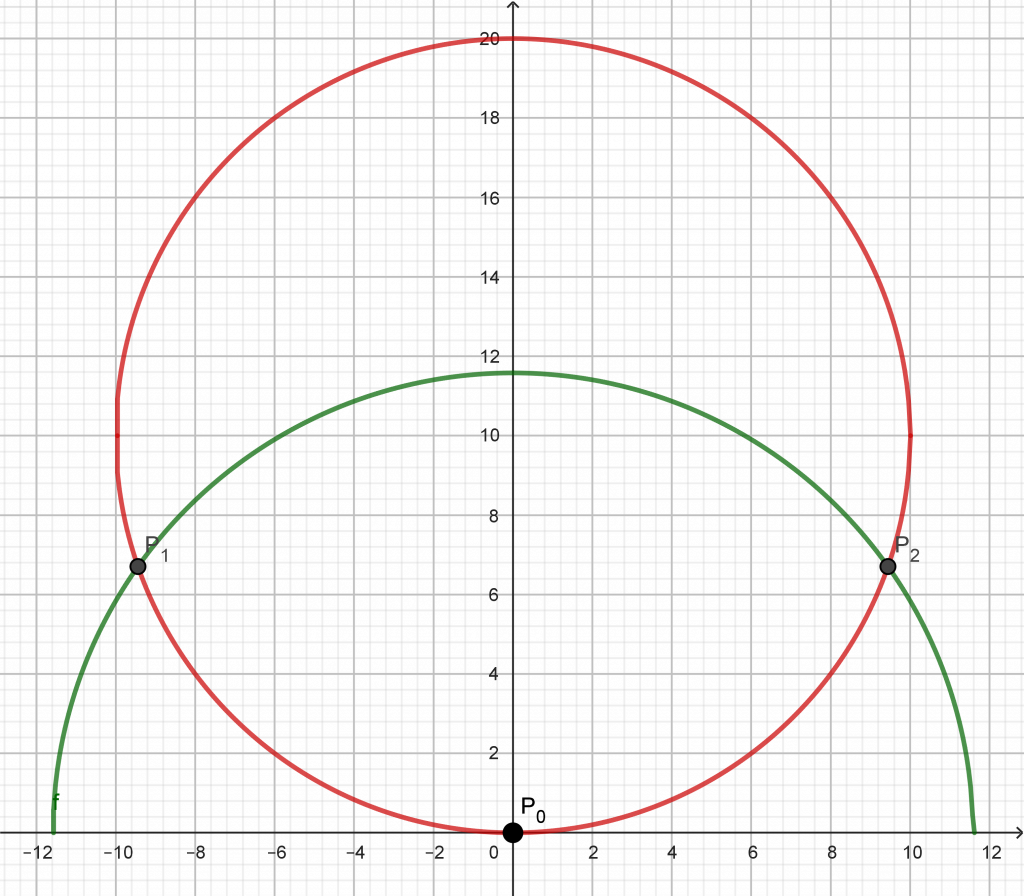
Als Schnittstellen des Kreises mit dem Graphen von f (= die x-Koordinaten von P₁ und P₂) ergeben sich

x₁ = -r·√(400-r²)/20 und x₂ = r·√(400-r²)/20

Den Wert des Integrals zwischen den beiden Graphen setzen wir gleich 50·π (das ist die Hälfte des Flächeninhalts der Wiese); und diese Gleichung lässt sich numerisch lösen:

r = 11,587284730…